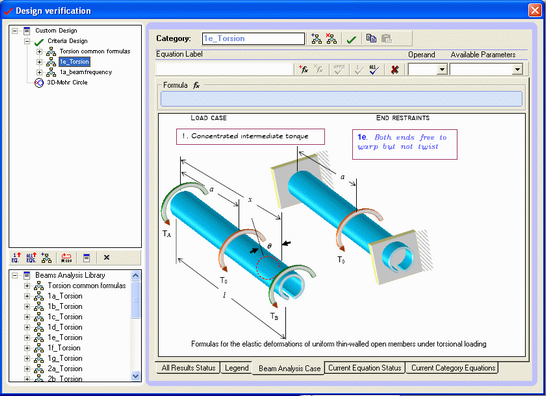
The “I” beam shown in the figure is subjected to a concentrated load of 40 000 lb, which is eccentric by 1 in from the vertical plane of the web. The flanges are 10 in by 0.5 in and the web is 12 in (Ref. Pilkey 1978). The ends experience no rotation, but are free to warp (case 1e_torsion in CustomDesign component see chapter 4). Determine the maximum normal and Shear stresses.
The Beam length is l=200 in, E=3 x 107 lb/in2, poison ration n=0.3
Reference results:
Cw= 3000 in6
Iy = 432 in4
J=1.333 in4
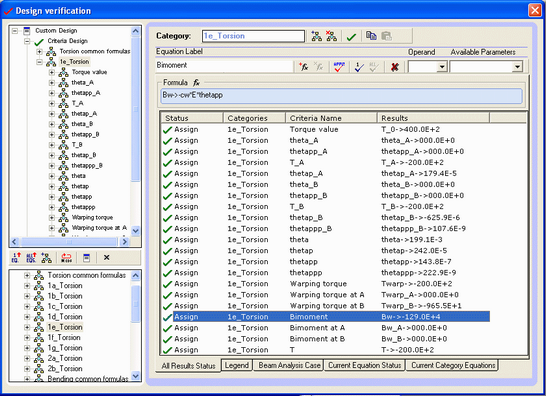
Bimoment B (x=l/2) = 1321200 lb.in2
Warping torque Tw(x=l/2) = 20000lb.in
The normal stress due to warping at the right edge of the top flange:
sw = - B*w/cw=-13212 lb/in2
The usual bending stress is found from a bending moment at midspan of M=Pl/4 =2000000lb.in
sx = 2000000 x 6/432 lb/in2=27.78 x 103 lb/in2
And the total axial stresses (at left and right top flange) is sx = 40990 lb/in2 or 14566 lb/in2
Reference: W.D. PILKEY, Modern Formulas for statics and dynamics, 1978, McGraw-Hill, Inc. Page 172, example 5.1.
Filename: Pilkey172.shd
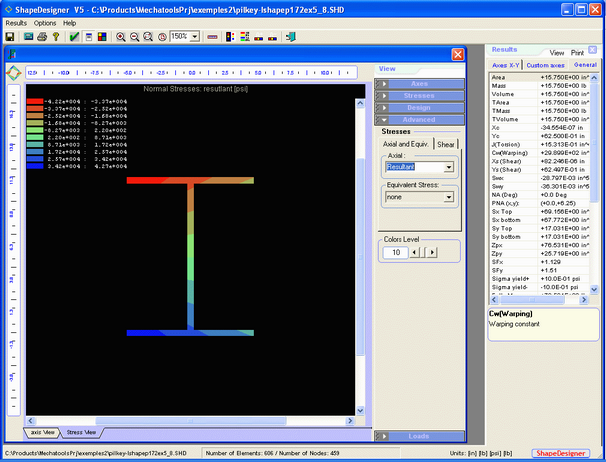
ShapeDesigner results
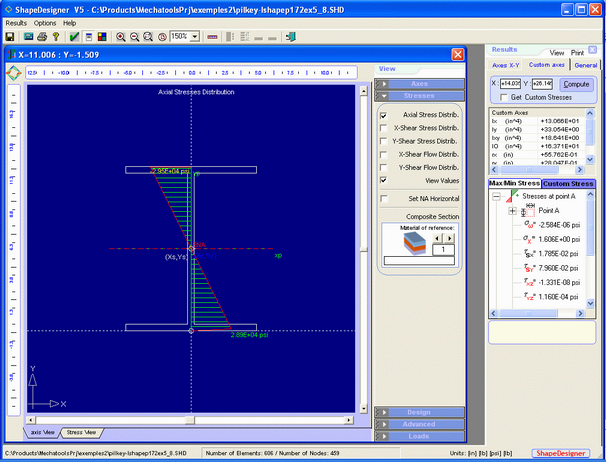
And the total axial stresses sx+sw
To compute internal force Bw and warping torque we select Design verification button to get the design Verification solver component: We select the 1e_torsion case (both ends free to warp but not twist)