From Vlasov’s theory the normal stresses
![]() and torsion shear stresses are given by:
and torsion shear stresses are given by:
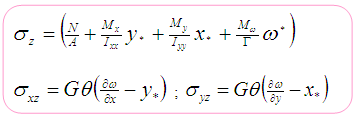
In which N=normal force,
![]() ,
,
![]() =bending moment with respect to the x and y centroid axes,
=bending moment with respect to the x and y centroid axes,
![]() =bimoment,
=bimoment,
![]() (x,y) de notes the “warping function” that represents the warping of the cross section from a plane and
(x,y) de notes the “warping function” that represents the warping of the cross section from a plane and
![]() ,
,
![]() are the coordinates of point that lie on the centroidal axes.
are the coordinates of point that lie on the centroidal axes.
The torque necessary to produce a twist
![]() is given by:
is given by:
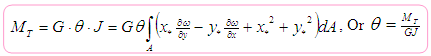
To obtain normal and shear stresses from equations given above, the following geometrical properties of cross-section must be calculated:
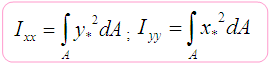 ;
;
![]() generalized warping function
generalized warping function
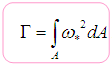 ; Principal sectorial moment of inertia, which is the famous warping constant
; Principal sectorial moment of inertia, which is the famous warping constant
Example of warping
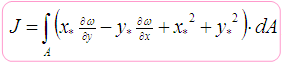 ; Torsion constant (Saint-Venant)
; Torsion constant (Saint-Venant)
Example of torsion
An axial load N x applied at the point P of the beam cross section, causes additional normal stress. In this case, it is necessary to replace the force with its force-couple equivalent at the centroid C. ShapeDesigner performs this step.
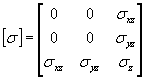
Saint-Venant assumed that the stresses,
![]() , are negligibly small, so that the stress tensor has the form:
, are negligibly small, so that the stress tensor has the form:
The fundamental assumption in Saint-Venant’s pure torsion analysis is that the cross sections are free to warp without restraint. This assumption is not satisfied if the beam has external supports, or if the beam is not prismatic, or when the torsional moment varies along the length of the beam. Even in these cases, Saint-Venant’s hypothesis of free warping gives good approximate results for beams with solid or closed thin-walled cross sections. For open thin-walled cross sections, however, this is no longer true. The twisting resistance of such sections is so small and the axial displacements are so large that the axial stress ÿ x caused by restrained warping cannot be neglected.
In pure torsion, with unrestrained warping, a reasonable approximation to the torsional shear stresses in an open thin-walled section is obtained by assuming a linear distribution across the thickness. The shear stress is then zero at the median line, and the shear flow is zero. For restrained warping analysis, the warping constant _is needed for use in the differential equation for the angle of twist. (See Beam analysis library in Custom design component for the use of this feature)